（本题共12分）有一小型自来水厂，蓄水池中已有水450吨，水厂每小时可向蓄水池注水80吨，同时蓄水池向居民小区供水，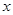
小时内供水总量为
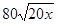吨。现在开始向池中注水并同时向居民小区供水，问：
（1）多少小时后蓄水池中的水量最少？
（2）如果蓄水池中存水量少于150吨时，就会出现供水紧张，那么有几个小时供水紧张？
相关试题
中，
，求
的值．
在角
的终边上，点
在角β的终边上，点
在角
终边上．
，
，
的值；
的值．
；
．
，
，函数
的最小值为
．
、
同时满足以下条件：
；②当
时，值域为
．若存在，求出
，
，函数
的最小值为
．
、
同时满足以下条件：
；
时，值域为
．若存在，求出推荐套卷
（本题共12分）有一小型自来水厂，蓄水池中已有水450吨，水厂每小时可向蓄水池注水80吨，同时蓄水池向居民小区供水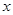，小时内供水总量为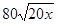吨。现在开始向池中注水并同时向居民小区供水，问：
（1）多少小时后蓄水池中的水量最少？
（2）如果蓄水池中存水量少于150吨时，就会出现供水紧张，那么有几个小时供水紧张？
粤公网安备 44130202000953号