学了统计知识后，小刚就本班同学上学“喜欢的出行方式”进行了一次调查。图（1）和图（2）是他根据采集的数据绘制的两幅不完整的统计图，请根据图中提供的信息解答以下问题：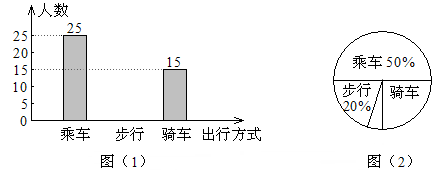
（1）补全条形统计图，并计算出“骑车”部分所对应的圆心角的度数；
（2）如果全年级共600名同学，请估算全年级步行上学的学生人数；
（3）若由3名“喜欢乘车”的学生，1名“喜欢步行”的学生，1名“喜欢骑车”的学生组队参加一项活动，欲从中选出2人担任组长（不分正副），求出2人都是“喜欢乘车”的学生的概率.
已知：
是一元二次方程
的两个实数
根．
求：
的值．考点：实数的运算；零指数幂；负整数指数幂．
专题：计算题．
分析：分别根据负整数指数幂、0指数幂、绝对值的性质及二次根式的化简计算出各数，再根据实数混合运算的法则进行计算即可．
解答：解：原式=2-1-3+2，
=0．
故答案为：0．
点评：本题考查的是实数的运算，熟知负整数指数幂、0指数幂、绝对值的性质及二次根式的化简是解答此题的关键．
答题：ZJX老师
如图，正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上，这四条直
线中相邻两条之间的距离依次为h1、h2、h3(h1＞0，h2＞0，h3＞0)．
(1)求证：h1＝h2；
(2)设正方形ABCD的面积为S，求证：S＝(h1＋h2)2＋h12；
(3)若h1＋h2＝1，当h1变化时，说明正方形ABCD的面积S随h1的变化情况．
在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋
转角为
(0°＜＜180°)，得到△A1B1C．
(1)如图1，当AB∥CB1时，设A1B1与BC相交于点D．证明：△A1CD是等边三角形；
(2)如图2，连接AA1、BB1，设△ACA1和△BCB1的面积分别为S1、S2．求证：S1∶S2＝1∶3；
(3)如图3，设AC的中点为E，A1B1的中点为P，AC＝a，连接EP．当＝°时，EP的长度最大，最大值为．
粤公网安备 44130202000953号