已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q到达点C时，P、Q两点都停止运动，设运动时间为t（s），解答下列问题：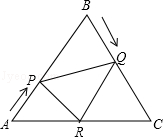
（1）当t=2时，判断△BPQ的形状，并说明理由；
（2）设△BPQ的面积为S（cm2），求S与t的函数关系式；
（3）作QR∥BA交AC于点R，连接PR，当t为何值时，△APR∽△PRQ．
相关试题
，其中
为不等式组
的整数解.如图所示，△ABC在平面直角坐标系中，将△ABC向下平移5个单位得到△A1B1C1，再将△A1B1C1绕点o顺时针旋转90°得到△A2B2C2，请作出△A1B1C1和△A2B2C2；
，求代数式
的值．
三个盘子里分别放了一些糖果，糖果数依次为
，
，
，记为
（
次操作后的糖果数记为
（
，
，
）．
________．相关知识点
推荐套卷
粤公网安备 44130202000953号