一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题: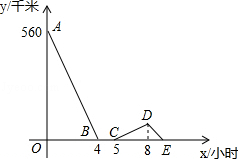
(1)甲乙两地之间的距离为 千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
相关知识点
推荐套卷
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲乙两地之间的距离为 千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.