为了更好地开展社团活动,丰富同学们的课余生活,现用分层抽样的方法从“模拟联合国”,“街舞”,“动漫”,“话剧”四个社团中抽取若干人组成校社团指导小组,有关数据见下表:(单位:人)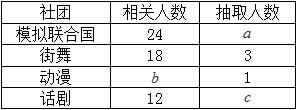
(Ⅰ)求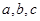 的值;
的值;
(Ⅱ)若从“模拟联合国”与“话剧”社团已抽取的人中选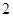 人担任指导小组组长,求这
人担任指导小组组长,求这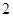 人分别来自这两个社团的概率.
人分别来自这两个社团的概率.
推荐套卷
为了更好地开展社团活动,丰富同学们的课余生活,现用分层抽样的方法从“模拟联合国”,“街舞”,“动漫”,“话剧”四个社团中抽取若干人组成校社团指导小组,有关数据见下表:(单位:人)
(Ⅰ)求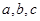 的值;
的值;
(Ⅱ)若从“模拟联合国”与“话剧”社团已抽取的人中选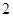 人担任指导小组组长,求这
人担任指导小组组长,求这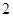 人分别来自这两个社团的概率.
人分别来自这两个社团的概率.