（本小题8分）已知圆
: 
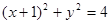和圆外一点
（1, 
）,
（1）若直线
经过原点
，且圆上恰有三个点到直线的距离为
,求直线的方程;
（2）若经过的直线
与圆相切，切点分别为
,求切线的方程及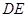
两切点所在的直线方程.
的不等式
．
与圆
相交于点
和点
。
与
的交点，且平行于直
的直线方程。
是实数,且
. 
求证:u为纯虚数; 
的最小值.
相关知识点
推荐套卷
（本小题8分）已知圆: 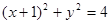和圆外一点（1, ）,
（1）若直线经过原点，且圆上恰有三个点到直线的距离为,求直线的方程;
（2）若经过的直线与圆相切，切点分别为,求切线的方程及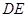两切点所在的直线方程.
粤公网安备 44130202000953号