如图，AB是半圆O的直径，点M是半径OA的中点，点P在线段AM上运动（不与点M重合），点Q在半圆O上运动，且总保持PQ=PO，过点Q作⊙O的切线交BA的延长线于点C．
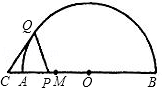
（1）当∠QPA=60°时，请你对△QCP的形状做出猜想，并给予证明；
（2）当QP⊥AB时，△QCP的形状是 三角形；
（3）由（1）、（2）得出的结论，请进一步猜想当点P在线段AM上运动到任何位置时，△QCP一定是 三角形．
相关试题
如图，要把边长为1的正方形ABCD的四个角（阴影部分）剪掉，得一四边形A1B1C1D1，试问怎样剪，才能使剩下的图形仍为正方形，且剩下图形的面积为原正方形面积的
，请说明理由.
如图，将矩形ABCD折叠，使顶点B与D重合，折痕为EF，连接BE、DF.
（1）四边形BEDF是什么四边形？为什么？
（2）若AB=6cm，BC=8cm，求折痕EF的长.
粤公网安备 44130202000953号