(本小题满分12分)(理科做)如图,四棱锥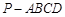 的底面
的底面 是直角梯形,
是直角梯形,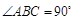 ,
, ,且
,且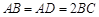 ,顶点
,顶点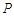 在底面
在底面 内的射影恰好落在
内的射影恰好落在 的中点
的中点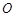 上.
上.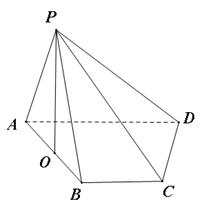
(1)求证: ;
;
(2)若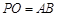 ,求直线
,求直线 与
与 所成角的 余弦值;
所成角的 余弦值;
(3)若平面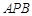 与平面
与平面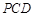 所成的二面角为
所成的二面角为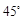 ,求
,求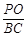 的值.
的值.
(文科做)设函数 .
.
(1)当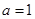 时,试求函数
时,试求函数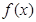 在区间
在区间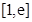 上的最大值;
上的最大值;
(2)当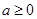 时,试求函数
时,试求函数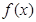 的单调区间.
的单调区间.
推荐套卷
(本小题满分12分)(理科做)如图,四棱锥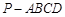 的底面
的底面 是直角梯形,
是直角梯形,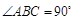 ,
, ,且
,且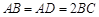 ,顶点
,顶点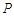 在底面
在底面 内的射影恰好落在
内的射影恰好落在 的中点
的中点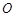 上.
上.
(1)求证: ;
;
(2)若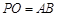 ,求直线
,求直线 与
与 所成角的 余弦值;
所成角的 余弦值;
(3)若平面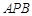 与平面
与平面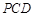 所成的二面角为
所成的二面角为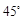 ,求
,求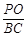 的值.
的值.
(文科做)设函数 .
.
(1)当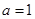 时,试求函数
时,试求函数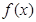 在区间
在区间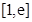 上的最大值;
上的最大值;
(2)当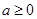 时,试求函数
时,试求函数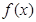 的单调区间.
的单调区间.