(本题满分14分)
如图,圆锥的顶点是S，底面中心为O.OC是与底面直径AB垂直的一条半径，D是母线SC的中点.
（1）求证：BC与SA不可能垂直.
（2）设圆锥的高为4，异面直线AD与BC所成角的余弦值为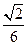
，求圆锥的体积.
相关试题
已知点O(0，0)，A(1，2)，B(4，5)及
，
求(1)t为何值时，P在x轴上？P在y轴上？P在第二象限。
(2)四边形OABP能否构成为平行四边形？若能，求出相应的t值；若不能，请说明理由。
(1,2),
(-3,2)，当k为何值时
与
平行?
，向量
，求
的最大值和最小值。推荐套卷
(本题满分14分)
如图,圆锥的顶点是S，底面中心为O.OC是与底面直径AB垂直的一条半径，D是母线SC的中点.
（1）求证：BC与SA不可能垂直.
（2）设圆锥的高为4，异面直线AD与BC所成角的余弦值为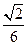，求圆锥的体积.
已知点O(0，0)，A(1，2)，B(4，5)及，
求(1)t为何值时，P在x轴上？P在y轴上？P在第二象限。
(2)四边形OABP能否构成为平行四边形？若能，求出相应的t值；若不能，请说明理由。
粤公网安备 44130202000953号