请仔细阅读以下材料:
已知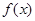 是定义在
是定义在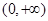 上的单调递增函数.
上的单调递增函数.
求证:命题“设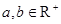 ,若
,若 ,则
,则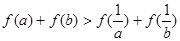 ”是真命题.
”是真命题.
证明 :因为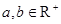 ,由
,由 得
得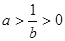 .
.
又因为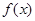 是定义在
是定义在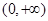 上的单调递增函数,
上的单调递增函数,
于是有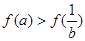 . ①
. ①
同理有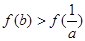 . ②
. ②
由①+ ②得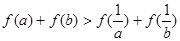 .
.
故,命题“设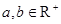 ,若
,若 ,则
,则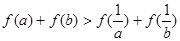 ”是真命题.
”是真命题.
请针对以上阅读材料中的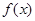 ,解答以下问题:
,解答以下问题:
(1)试用命题的等价性证明:“设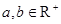 ,若
,若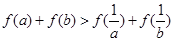 ,则:
,则: ”是真命题;
”是真命题;
(2)解关于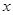 的不等式
的不等式 (其中
(其中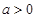 ).
).
相关知识点
推荐套卷
请仔细阅读以下材料:
已知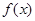 是定义在
是定义在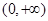 上的单调递增函数.
上的单调递增函数.
求证:命题“设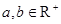 ,若
,若 ,则
,则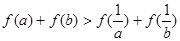 ”是真命题.
”是真命题.
证明 :因为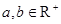 ,由
,由 得
得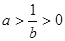 .
.
又因为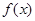 是定义在
是定义在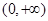 上的单调递增函数,
上的单调递增函数,
于是有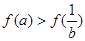 . ①
. ①
同理有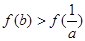 . ②
. ②
由①+ ②得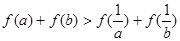 .
.
故,命题“设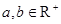 ,若
,若 ,则
,则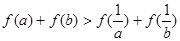 ”是真命题.
”是真命题.
请针对以上阅读材料中的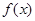 ,解答以下问题:
,解答以下问题:
(1)试用命题的等价性证明:“设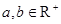 ,若
,若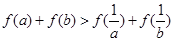 ,则:
,则: ”是真命题;
”是真命题;
(2)解关于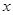 的不等式
的不等式 (其中
(其中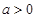 ).
).