复习“全等三角形”的知识时，老师布置了一道作业题：“如图所示，已知在△ABC中，AB=AC，P是△ABC内任意一点.将AP绕A顺时旋转于AQ，使∠QAP=∠BAC，连接BQ，CP则BQ=CP.”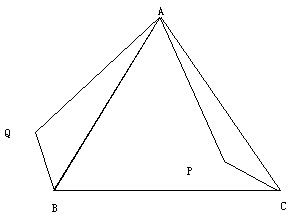
相关试题
如图所示是甲、乙两人追赶过程中路程和时间之间的函数关系图象，由图象回答下列问题：
（1）谁追赶谁?甲、乙两人谁出发早?早几小时?
（2）甲出发几小时后两人相遇?此时他们走了多远?
相关知识点
推荐套卷
复习“全等三角形”的知识时，老师布置了一道作业题：“如图所示，已知在△ABC中，AB=AC，P是△ABC内任意一点.将AP绕A顺时旋转于AQ，使∠QAP=∠BAC，连接BQ，CP则BQ=CP.”
如图所示是甲、乙两人追赶过程中路程和时间之间的函数关系图象，由图象回答下列问题：
（1）谁追赶谁?甲、乙两人谁出发早?早几小时?
（2）甲出发几小时后两人相遇?此时他们走了多远?
粤公网安备 44130202000953号