（满分5分）如图，货轮D在航行过程中，发现灯塔A在它的南偏东60°的方向上．同时，在货轮D的北偏西30°、西北方向上又发现了客轮B和海岛C．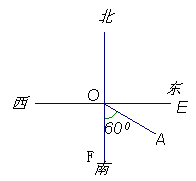
（1）仿照表示灯塔方位的方法，在图中画出表示客轮B和海岛C方向的射线；
（2）在（1）的条件下填空：
∠BOC=_______，∠BOA=______；和∠AOF互余的角为：_______________．
相关试题
（满分5分）如图，货轮D在航行过程中，发现灯塔A在它的南偏东60°的方向上．同时，在货轮D的北偏西30°、西北方向上又发现了客轮B和海岛C．
（1）仿照表示灯塔方位的方法，在图中画出表示客轮B和海岛C方向的射线；
（2）在（1）的条件下填空：
∠BOC=_______，∠BOA=______；和∠AOF互余的角为：_______________．
成立吗？并说明理由．
的外接圆，
，
为⊙O的直径，且
，连结
．求BC的长． 
化为
的形式（其中
为常数
），写出这个二次函数图象的顶点坐标 和对称轴方程，并在直角坐标系中画出他的示意图．
粤公网安备 44130202000953号