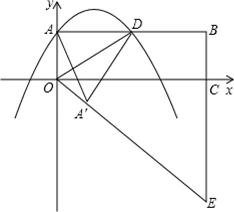
如图,在平面直角坐标系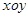 中,矩形
中,矩形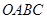 的边
的边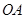 、
、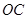 分别在
分别在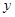 轴和
轴和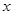 轴的正半轴上,且长分别为
轴的正半轴上,且长分别为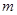 、
、
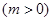 ,
, 为边
为边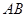 的中点,一抛物线
的中点,一抛物线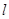 经过点
经过点 、
、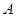 及点
及点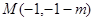 .
.
(1)求抛物线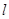 的解析式(用含
的解析式(用含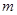 的式子表示);[来#&%^源:@中教网]
的式子表示);[来#&%^源:@中教网]
(2)把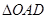 沿直线
沿直线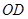 折叠后点
折叠后点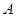 落在点
落在点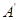 处,连接
处,连接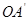 并延长与线段
并延长与线段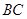 的延长线交于点
的延长线交于点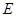 ,若抛物线
,若抛物线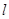 与线段
与线段 相交,求实数
相交,求实数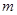 的取值范围;
的取值范围;
(3)在满足(2)的条件下,求出抛物线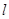 顶点
顶点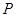 到达最高位置时的坐标.
到达最高位置时的坐标.
相关知识点
推荐套卷
如图,在平面直角坐标系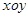 中,矩形
中,矩形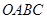 的边
的边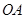 、
、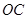 分别在
分别在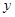 轴和
轴和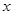 轴的正半轴上,且长分别为
轴的正半轴上,且长分别为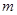 、
、
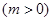 ,
, 为边
为边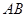 的中点,一抛物线
的中点,一抛物线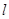 经过点
经过点 、
、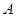 及点
及点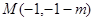 .
.
(1)求抛物线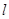 的解析式(用含
的解析式(用含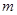 的式子表示);[来#&%^源:@中教网]
的式子表示);[来#&%^源:@中教网]
(2)把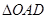 沿直线
沿直线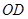 折叠后点
折叠后点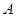 落在点
落在点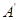 处,连接
处,连接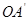 并延长与线段
并延长与线段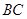 的延长线交于点
的延长线交于点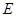 ,若抛物线
,若抛物线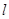 与线段
与线段 相交,求实数
相交,求实数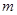 的取值范围;
的取值范围;
(3)在满足(2)的条件下,求出抛物线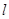 顶点
顶点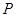 到达最高位置时的坐标.
到达最高位置时的坐标.