细心观察下列图形,认真分析各式,然后解答问题:s1,s2, s3,…表示各个三角形的面积
OA22=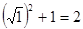
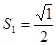 ;
;
OA32=12+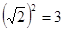
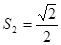 ;
;
OA42=12+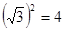
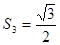
…… ……
(1)推算出OA10的长.
(2) 请用含有n(n是正整数)的等式表示上述的两个变化规律.
(3)若一个三角形的面积是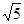 ,通过计算说明它是第几个三角形?
,通过计算说明它是第几个三角形? 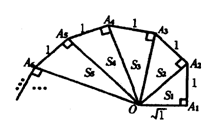
相关知识点
推荐套卷
细心观察下列图形,认真分析各式,然后解答问题:s1,s2, s3,…表示各个三角形的面积
OA22=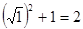
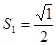 ;
;
OA32=12+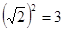
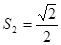 ;
;
OA42=12+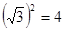
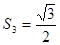
…… ……
(1)推算出OA10的长.
(2) 请用含有n(n是正整数)的等式表示上述的两个变化规律.
(3)若一个三角形的面积是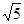 ,通过计算说明它是第几个三角形?
,通过计算说明它是第几个三角形? 