已知圆 的圆心在坐标原点
的圆心在坐标原点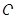 ,且恰好与直线
,且恰好与直线 相切,设点A为圆上一动点,
相切,设点A为圆上一动点, 轴于点
轴于点 ,且动点
,且动点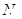 满足
满足 ,设动点
,设动点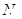 的轨迹为曲线
的轨迹为曲线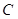
(Ⅰ)求曲线C的方程;
(Ⅱ)直线 交曲线
交曲线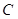 于不同的
于不同的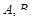 两点,
两点,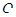 是坐标原点,求
是坐标原点,求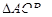 面积的最大值.
面积的最大值.
相关知识点
推荐套卷
已知圆 的圆心在坐标原点
的圆心在坐标原点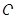 ,且恰好与直线
,且恰好与直线 相切,设点A为圆上一动点,
相切,设点A为圆上一动点, 轴于点
轴于点 ,且动点
,且动点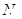 满足
满足 ,设动点
,设动点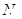 的轨迹为曲线
的轨迹为曲线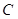
(Ⅰ)求曲线C的方程;
(Ⅱ)直线 交曲线
交曲线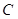 于不同的
于不同的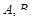 两点,
两点,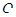 是坐标原点,求
是坐标原点,求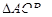 面积的最大值.
面积的最大值.