(本题8分)某文具店销售一种进价为每本10元的笔记本,为获得高利润,以不低于进价进行销售,结果发现,每月销售量 与销售单价
与销售单价 之间的关系可以近似地看作一次函数:
之间的关系可以近似地看作一次函数: ,物价部门规定这种笔记本每本的销售单价不得高于18元.
,物价部门规定这种笔记本每本的销售单价不得高于18元.
(1)当每月销售量为70本时,获得的利润为多少元?
(2)该文具店这种笔记本每月获得利润为 元,求每月获得的利润
元,求每月获得的利润 元与销售单价
元与销售单价 之间的函数关系式,并写出自变量的取值范围.
之间的函数关系式,并写出自变量的取值范围.
(3)当销售单价定为多少元时,每月可获得最大利润,最大利润为多少元?
相关知识点
推荐套卷
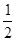 ,我可以知道你计算的结果是2.”
,我可以知道你计算的结果是2.” 的值与其中某个字母的取值无关,你能求出哪一个字母的值?此时这个字母的值是多少?
的值与其中某个字母的取值无关,你能求出哪一个字母的值?此时这个字母的值是多少?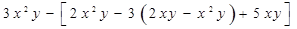 ,其中
,其中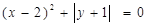
 +
+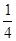 +
+ ).
).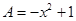 ,
, ,求2A-B.
,求2A-B. 粤公网安备 44130202000953号
粤公网安备 44130202000953号