(本小题满分16分)
(1)求右焦点坐标是 ,且经过点
,且经过点 的椭圆的标准方程.
的椭圆的标准方程.
(2)已知椭圆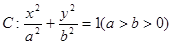 ,设斜率为
,设斜率为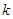 的直线
的直线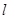 交椭圆
交椭圆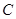 于
于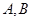 两点,
两点, 的中点为
的中点为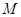 ,证明:当直线
,证明:当直线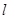 平行移动时,动点
平行移动时,动点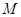 在一条过原点的定直线上.
在一条过原点的定直线上.
(3)利用(2)中所揭示的椭圆几何性质,用作图方法找出图中的定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.
推荐套卷
(本小题满分16分)
(1)求右焦点坐标是 ,且经过点
,且经过点 的椭圆的标准方程.
的椭圆的标准方程.
(2)已知椭圆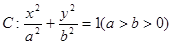 ,设斜率为
,设斜率为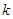 的直线
的直线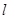 交椭圆
交椭圆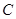 于
于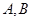 两点,
两点, 的中点为
的中点为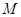 ,证明:当直线
,证明:当直线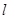 平行移动时,动点
平行移动时,动点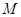 在一条过原点的定直线上.
在一条过原点的定直线上.
(3)利用(2)中所揭示的椭圆几何性质,用作图方法找出图中的定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.