某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原始分均为100分．前6名选手的得分如下：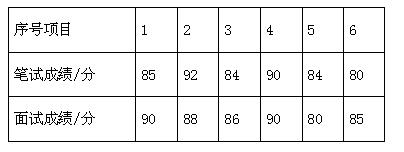
根据规定，笔试成绩和面试成绩分别按一定的百分比折算成综合成绩（综合成绩的满分仍为100分）．
（1）求出这6名选手笔试成绩的中位数、众数；
（2）现得知1号选手的综合成绩为88分，求笔试成绩和面试成绩各占的百分比；
（3）求出其余五名选手的综合成绩，并以综合成绩排序确定前两名人选．
相关试题
已知：如图，在△ABC中，AB=AC，∠BAC=30°．点D为△ABC内一点，且DB=DC，∠DCB=30°，点E为BD延长线上一点，且AE=AB．
（1）求∠ADE的度数；
（2）若点M在DE上，且DM=DA，求证：ME=DC．
与
轴交于点A，与
轴交于点B．已知：如图1，长方形ABCD中，AB=2，动点P在长方形的边BC，CD，DA上沿
的方向运动，且点P与点A，B都不重合．图2是此运动过程中，△ABP的面积
与点P经过的路程
之间的函数图象的一部分．
请结合以上信息回答下列问题：
长方形ABCD中，边BC的长为________；
若长方形ABCD中，M为CD边的中点，当点P运动到与点M重合时，
=________，=________；当
时，与之间的函数关系式是___________________；利用第（3）问求得的结论，在图2中将相应的
与的函数图象补充完整．
．
粤公网安备 44130202000953号