（本小题满分12分）某人上午7：00乘汽车以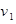
千米/小时
匀速从A地出发到距300公里的B地，在B地不作停留，然后骑摩托车以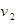
千米/小时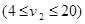
匀速从B地出发到距50公里的C地，计划在当天16：00至21：00到达C地。设乘汽车、骑摩托车的时间分别是x,y小时，如果已知所需的经费
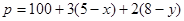元，那么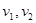
分别是多少时走的最经济，此时花费多少元？
相关试题
中，椭圆
的中心为原点，焦点
在
轴上，离心率为
，过点
的直线
交椭圆
两点，且
的周长为16，求椭圆
：
的离心率
，
、
为其左右焦点，点
在
，
，
是坐标原点．
的直线
与双曲线
两点，求
的取值范围．
中，点
分别是
的中点．
．
与
所成角的余弦值．
的值；推荐套卷
（本小题满分12分）某人上午7：00乘汽车以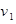千米/小时匀速从A地出发到距300公里的B地，在B地不作停留，然后骑摩托车以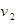千米/小时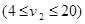匀速从B地出发到距50公里的C地，计划在当天16：00至21：00到达C地。设乘汽车、骑摩托车的时间分别是x,y小时，如果已知所需的经费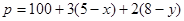元，那么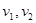分别是多少时走的最经济，此时花费多少元？
粤公网安备 44130202000953号