正方形ABCD中,将一个直角三角板的直角顶点与点A重合,一条直角边与边BC交于点E(点E不与点B和点C重合),另一条直角边与边CD的延长线交于点F.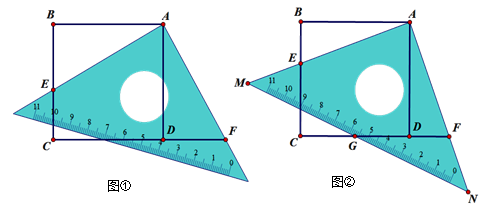
(1)如图①,求证:AE="AF;"
(2)如图②,此直角三角板有一个角是45°,它的斜边MN与边CD交于G,且点G是斜边MN的中点,连接EG,求证:EG="BE+DG;"
(3)在(2)的条件下,如果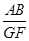 =
= 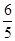 ,那么点G是否一定是边CD的中点?请说明你的理由.
,那么点G是否一定是边CD的中点?请说明你的理由.
相关知识点
推荐套卷
正方形ABCD中,将一个直角三角板的直角顶点与点A重合,一条直角边与边BC交于点E(点E不与点B和点C重合),另一条直角边与边CD的延长线交于点F.
(1)如图①,求证:AE="AF;"
(2)如图②,此直角三角板有一个角是45°,它的斜边MN与边CD交于G,且点G是斜边MN的中点,连接EG,求证:EG="BE+DG;"
(3)在(2)的条件下,如果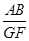 =
= 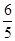 ,那么点G是否一定是边CD的中点?请说明你的理由.
,那么点G是否一定是边CD的中点?请说明你的理由.