在正方形网格中建立如图所示的平面直角坐标系xoy．△ABC的三个顶点都在格点上，点A、B、C的坐标分别是A（4，4 ）、B（1，2 ）、C（3，2 ），请解答下列问题；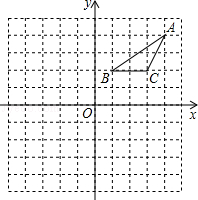
（1）将△ABC向下平移5个单位长度，画出平移后的△A1B1C1；
（2）画出△A1B1C1关于y轴对称的△A2B2C2；
（3）将△ABC绕点O逆时针旋转90°，画出旋转后的的△A3B3C3．并写出点A3的坐标：A3（ ， ）；
相关试题
（本题6分） 某厂接到在规定时间内生产1500台冰箱的任务．在生产了300台冰箱后，厂家把工作效率提高到原来的1.5倍，于是提前4天完成任务，求原来每天生产多少台冰箱？
（本题6分）如图，一架2.5米长的梯子AB，斜靠在一竖直的墙AO上，这时梯足B到墙底端O的距离为0.7米, 如果梯子的顶端沿墙下滑0.4米，那么梯足将向外移多少米？
（本题6分）如图，在平面直角坐标系xoy中，A(－1,4)，B(－2，0)，C(－4,2)
(1)、请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；
(2)、直接写出A′，B′，C′三点的坐标：A′( )，B′( )，C′( )
△ABC的面积=．
)÷(
)，再从-2，2，0三个数中选一个适当的数作为a的值代入求值.
－4
.相关知识点
推荐套卷
粤公网安备 44130202000953号