自新冠肺炎疫情爆发以来,我国人民上下一心,团结一致,基本控制住了疫情.然而,全球新冠肺炎疫情依然严重,境外许多国家的疫情尚在继续蔓延,疫情防控不可松懈.如图是某国截止5月31日新冠病毒感染人数的扇形统计图和折线统计图.
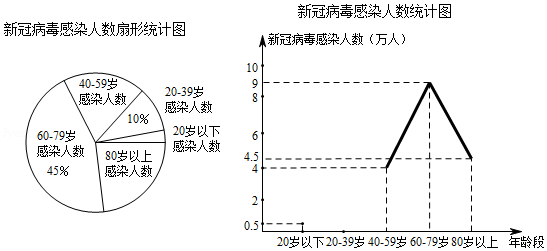
根据上面图表信息,回答下列问题:
(1)截止5月31日该国新冠肺炎感染总人数累计为 万人,扇形统计图中
岁感染人数对应圆心角的度数为
;
(2)请直接在图中补充完整该国新冠肺炎感染人数的折线统计图;
(3)在该国所有新冠肺炎感染病例中随机地抽取1人,求该患者年龄为60岁或60岁以上的概率;
(4)若该国感染病例中从低到高各年龄段的死亡率依次为
、
、
、
、
,求该国新冠肺炎感染病例的平均死亡率.