(本题12分)某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制)(均为整数)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.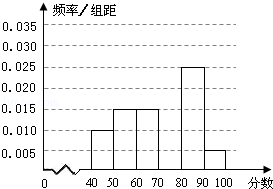
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试的平均分;
(3)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,在[70,100]记1分,用X表示抽取结束后的总记分,求X的分布列和数学期望.
相关知识点
推荐套卷
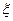 为取出的4个球中红
为取出的4个球中红 球的个数,求
球的个数,求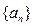 的公比为
的公比为 ,首项为
,首项为 ,其前
,其前 项的和为
项的和为 .数列
.数列 的前
的前 , 数列
, 数列 的前
的前
 ,
, ,求
,求 的通项公式;(Ⅱ)①当
的通项公式;(Ⅱ)①当 与
与 的大小; ②当
的大小; ②当 ,问是否存在常数
,问是否存在常数 (与n无关),使得等式
(与n无关),使得等式 恒成立,若存在,求出
恒成立,若存在,求出 为正方形,
为正方形, 为矩形,
为矩形, 平面
平面 为
为 的中点(Ⅰ)求证
的中点(Ⅰ)求证 平面
平面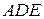 ;(Ⅱ)求证平面
;(Ⅱ)求证平面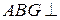 平面
平面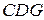 ;
;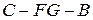 的余弦植。
的余弦植。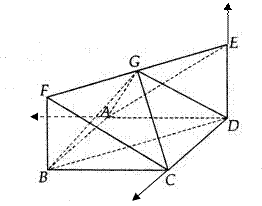
 ,
, ,
, 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为 、
、 ,设
,设 为坐标原点,点
为坐标原点,点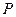 的坐标为
的坐标为 ,记
,记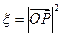
 的最大值,并求事件“
的最大值,并求事件“ 已知函数
已知函数
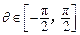 ,且
,且 ,求
,求 的值
的值 ,且△ABC的面积为
,且△ABC的面积为 ,求sinA+sinB的值
,求sinA+sinB的值 粤公网安备 44130202000953号
粤公网安备 44130202000953号