利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
(1)当每吨售价是240元时,计算此时的月销售量;
(2)在遵循“薄利多销”的原则下,问每吨材料售价为多少时,该经销店的月利润为9000元?
相关知识点
推荐套卷
 ,直线y=
,直线y= 经过点C,交y轴于点G。
经过点C,交y轴于点G。
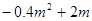 ;
;

 (a<0)与反比例函数
(a<0)与反比例函数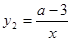 的图象有两个公共点,其中一个公共点的纵坐标为4.
的图象有两个公共点,其中一个公共点的纵坐标为4. .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号