如图,三棱柱ABC-A1B1C1的所有棱长都是2,又AA1⊥平面ABC,D,E分别是AC,CC1的中点.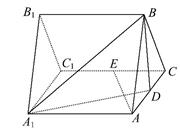
(1)求证:AE⊥平面A1BD.
(2)求二面角D-BA1-A的余弦值.
(3)求点B1到平面A1BD的距离.
相关试题
的定义域为实数集
，且
上是增函数，当
时，是否存在实数
，使
对所有的
恒成立？若存在，求出实数
，不等式
的解集为
. 
的解析式；
；
在
上是增函数，求实数
的取值范围.
，其中向量
，
，
，
的单调递减区间及对称轴方程；
成立的
的取值范围.
的定义域为集合
，求：当
时，函数
的最值，并指出
取得最值时的
值.
，
, 且
的值.（2）求
的大小.相关知识点
推荐套卷
如图,三棱柱ABC-A1B1C1的所有棱长都是2,又AA1⊥平面ABC,D,E分别是AC,CC1的中点.
(1)求证:AE⊥平面A1BD.
(2)求二面角D-BA1-A的余弦值.
(3)求点B1到平面A1BD的距离.
粤公网安备 44130202000953号