由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高.然而也有部分公众对该活动的实际效果与负面影响提出了疑问.对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
|
支持
|
保留
|
不支持
|
20岁以下
|
800
|
450
|
200
|
20岁以上(含20岁)
|
100
|
150
|
300
|
(1)在所有参与调查的人中,用分层抽样的方法抽取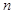 个人,已知从“支持”态度的人中抽取了45人,求
个人,已知从“支持”态度的人中抽取了45人,求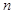 的值;
的值;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任意选取2人,求至少有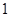 人20岁以下的概率;
人20岁以下的概率;