（本小题满分14分）已知中心在坐标原点O，焦点在x轴上的椭圆C的离心率为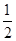
，且经过点
．
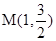(1)求椭圆C的方程；
(2)若F是椭圆C的右焦点，过F的直线交椭圆C于M、N两点，T为直线x＝4上任意一点，且T不在x轴上，
(ⅰ)求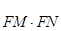
的取值范围；
(ⅱ)若OT平分线段MN，证明：TF⊥MN（其中O为坐标原点）.
，方程
的两个根
满足
.当
时，证明
.
，若
，
，
, 试证明：对于任意
，有
.
的解集为
，求实数p与q的值．
，当y＜0时，有
，解关于x的不等式
推荐套卷
（本小题满分14分）已知中心在坐标原点O，焦点在x轴上的椭圆C的离心率为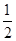，且经过点．
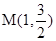(1)求椭圆C的方程；
(2)若F是椭圆C的右焦点，过F的直线交椭圆C于M、N两点，T为直线x＝4上任意一点，且T不在x轴上，
(ⅰ)求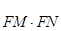的取值范围；
(ⅱ)若OT平分线段MN，证明：TF⊥MN（其中O为坐标原点）.
粤公网安备 44130202000953号