定义：如图1，点C在线段AB上，若满足AC2=BC•AB，则称点C为线段AB的黄金分割点．如图2，△ABC中，AB=AC=1，∠A=36°，BD平分∠ABC交AC于点D．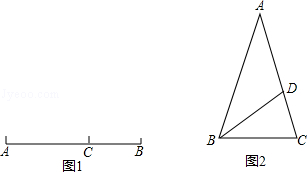
（1）求证：点D是线段AC的黄金分割点；
（2）求出线段AD的长．
，其中x=﹣1．
；
；
≤
相关知识点
推荐套卷
定义：如图1，点C在线段AB上，若满足AC2=BC•AB，则称点C为线段AB的黄金分割点．如图2，△ABC中，AB=AC=1，∠A=36°，BD平分∠ABC交AC于点D．
（1）求证：点D是线段AC的黄金分割点；
（2）求出线段AD的长．
粤公网安备 44130202000953号