（本题8分）如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A（-3,2）,B（0,4）,C（0,2）.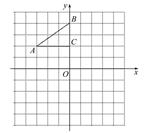
（1）将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为（0,-4）,画出平移后对应的△A2B2C2.
（2）若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标.
（3）在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
的值：（本题每小题4分，共8分）
；
；（本题6分）先看数列：1，2，4，8，…，263．从第二项起，每一项与它的前一项的比都等于2，象这样，一个数列：a1，a2，a3，…，an﹣1，an；从它的第二项起，每一项与它的前一项的比都等于一个常数q，那么这个数列就叫等比数列，q叫做等比数列的公比．
根据你的阅读，回答下列问题：
（1）请你写出一个等比数列，并说明公比是多少？
（2）请你判断下列数列是否是等比数列，并说明理由；
，
，
，
，…；
（3）有一个等比数列a1，a2，a3，…，an﹣1，an；已知a1=5，q=﹣3；请求出它的第25项a25．（结果不需化简,可以保留乘方的形式）
（本题6分）某工艺厂计划一周生产工艺品2100个，平均每天生产300个，但实际每天生产量与计划相比有出入．下表是某周的生产情况（超产记为正、减产记为负）：
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减（单位：个） |
+5 |
﹣2 |
﹣5 |
+15 |
﹣10 |
﹣6 |
﹣9 |
（1）写出该厂星期三生产工艺品的数量；
（2）本周产量中最多的一天比最少的一天多生产多少个工艺品？
（3）请求出该工艺厂在本周实际生产工艺品的数量；
（4）已知该厂实行每周计件工资制，每生产一个工艺品可得60元，若超额完成任务，则超过部分每个另奖50元，少生产一个扣80元．试求该工艺厂在这一周应付出的工资总额．
（本题5分）定义一种新运算：观察下列式：
1⊙3＝1×4+3＝7； 3⊙（－1）＝3×4－1＝11；
5⊙4＝5×4+4＝24； 4⊙（－3）＝4×4－3＝13；……
（1）根据上面的规律，请你想一想：a⊙b＝ ；
（2）若a⊙（－2b）＝6，请计算（a－b）⊙（2a+b）的值．
时，求多项式
的值”．小敏指出，题中给出的条件
，
是多余的，她的说法有道理吗？为什么？
粤公网安备 44130202000953号