(本题满分14分) 己知函数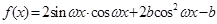 (其中
(其中 )的最大值为
)的最大值为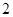 ,直线
,直线 是
是 图象的任意两条对称轴,且
图象的任意两条对称轴,且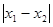 的最小值为
的最小值为 .
.
(1)求函数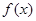 的单调增区间;
的单调增区间;
(2)若 ,求
,求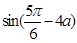 的值;
的值;
(3)对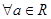 ,在区间
,在区间 上
上 有且只有
有且只有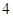 个零点,请直接写出满足条件的所有
个零点,请直接写出满足条件的所有 的值并把上述结论推广到一般情况.(不要求证明)
的值并把上述结论推广到一般情况.(不要求证明)
相关知识点
推荐套卷
(本题满分14分) 己知函数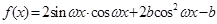 (其中
(其中 )的最大值为
)的最大值为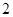 ,直线
,直线 是
是 图象的任意两条对称轴,且
图象的任意两条对称轴,且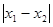 的最小值为
的最小值为 .
.
(1)求函数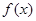 的单调增区间;
的单调增区间;
(2)若 ,求
,求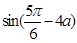 的值;
的值;
(3)对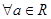 ,在区间
,在区间 上
上 有且只有
有且只有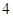 个零点,请直接写出满足条件的所有
个零点,请直接写出满足条件的所有 的值并把上述结论推广到一般情况.(不要求证明)
的值并把上述结论推广到一般情况.(不要求证明)