在一次数学测验活动中,小明到操场测量旗杆AB的高度,他手拿一支铅笔MN,边观察边移动(铅笔MN始终与地面垂直)。如示意图,当小明移动到D点时,眼睛C与铅笔、旗杆的顶端M、A共线,同时,眼睛C与它们的底端N、B也恰好共线。此时,测得DB=50m,小明的眼睛C到铅笔的距离为0.65m,铅笔MN的长为0.16m,请你帮助小明计算出旗杆AB的高度(结果精确到0.1m)。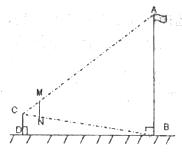
相关知识点
推荐套卷
在一次数学测验活动中,小明到操场测量旗杆AB的高度,他手拿一支铅笔MN,边观察边移动(铅笔MN始终与地面垂直)。如示意图,当小明移动到D点时,眼睛C与铅笔、旗杆的顶端M、A共线,同时,眼睛C与它们的底端N、B也恰好共线。此时,测得DB=50m,小明的眼睛C到铅笔的距离为0.65m,铅笔MN的长为0.16m,请你帮助小明计算出旗杆AB的高度(结果精确到0.1m)。