武汉某公司策划部进行调查后发现:如果单独投资A种产品,则所获利润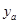 (万元)与投资金额
(万元)与投资金额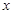 (万元)之间的关系图像如图1所示;如果单独投资B种产品,则所获利润
(万元)之间的关系图像如图1所示;如果单独投资B种产品,则所获利润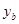 (万元)与投资金额
(万元)与投资金额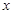 (万元)之间的关系图像如图2所示.
(万元)之间的关系图像如图2所示.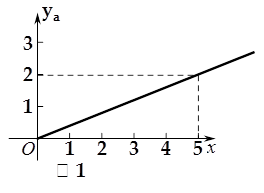
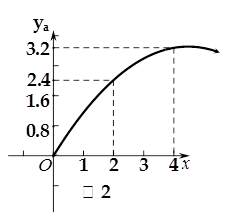
(1)请分别求出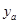 、
、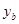 与
与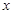 之间的函数表达式;
之间的函数表达式;
(2)若公司计划A、B两种产品共投资10万元,请你帮助该公司设计一个能获得最大利润的投资方案,并求出此方案所获得的最大利润.
相关知识点
推荐套卷
武汉某公司策划部进行调查后发现:如果单独投资A种产品,则所获利润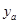 (万元)与投资金额
(万元)与投资金额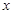 (万元)之间的关系图像如图1所示;如果单独投资B种产品,则所获利润
(万元)之间的关系图像如图1所示;如果单独投资B种产品,则所获利润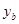 (万元)与投资金额
(万元)与投资金额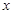 (万元)之间的关系图像如图2所示.
(万元)之间的关系图像如图2所示.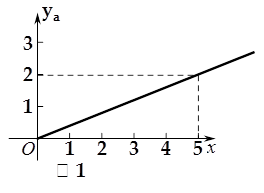
(1)请分别求出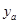 、
、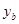 与
与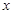 之间的函数表达式;
之间的函数表达式;
(2)若公司计划A、B两种产品共投资10万元,请你帮助该公司设计一个能获得最大利润的投资方案,并求出此方案所获得的最大利润.