(本小题满分10分)某校要进行特色学校评估验收,有甲、乙、丙、丁、戊五位评估员将随机去 三个不同的班级进行随班听课,要求每个班级至少有一位评估员.
三个不同的班级进行随班听课,要求每个班级至少有一位评估员.
(1)求甲、乙同时去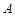 班听课的概率;
班听课的概率;
(2)设随机变量 为这五名评估员去
为这五名评估员去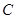 班听课的人数,求
班听课的人数,求 的分布列和数学期望.
的分布列和数学期望.
推荐套卷
(本小题满分10分)某校要进行特色学校评估验收,有甲、乙、丙、丁、戊五位评估员将随机去 三个不同的班级进行随班听课,要求每个班级至少有一位评估员.
三个不同的班级进行随班听课,要求每个班级至少有一位评估员.
(1)求甲、乙同时去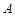 班听课的概率;
班听课的概率;
(2)设随机变量 为这五名评估员去
为这五名评估员去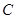 班听课的人数,求
班听课的人数,求 的分布列和数学期望.
的分布列和数学期望.