（本题共13分，第（Ⅰ）问5分，第（Ⅱ）问8分）
今年3月1日，重庆某中学50位学生参加了“北约联盟”的自主招生考试．这50位同学的数学成绩的频率分布直方图如图所示，其中成绩分组区间是：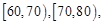
．
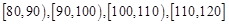（Ⅰ）求图中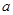
的值；
（Ⅱ）从成绩不低于100分的学生中随机选取2人，该2人中成绩在110分以上（含110分）的人数记为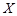
，求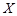的分布列和数学期望．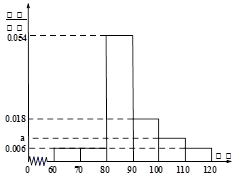
的最小正周期；
时,求函数
，
．
的最大值；
，求
的值.
，
，求
的值
的值;
求△ABC的面积S.推荐套卷
（本题共13分，第（Ⅰ）问5分，第（Ⅱ）问8分）
今年3月1日，重庆某中学50位学生参加了“北约联盟”的自主招生考试．这50位同学的数学成绩的频率分布直方图如图所示，其中成绩分组区间是：．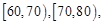
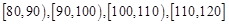（Ⅰ）求图中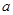的值；
（Ⅱ）从成绩不低于100分的学生中随机选取2人，该2人中成绩在110分以上（含110分）的人数记为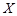，求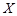的分布列和数学期望．
粤公网安备 44130202000953号