（本小题满分14分）已知圆C的圆心在坐标原点，且与直线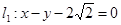
相切.
（1）求直线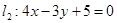
被圆C所截得的弦AB的长；
（2）过点G（1,3）作两条与圆C相切的直线，切点分别为M,N，求直线MN的方程；
（3）若与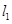直线
垂直的直线
不过点R（1,-1），且与圆C交于不同的两点P，Q.若∠PRQ为钝角，求直线的纵截距的取值范围．
相关试题
被双曲线
截得的弦长；
的直线被双曲线
在平面直角坐标系中，点
的横、纵坐标满足
。
的所有坐标；
轴上的概率；
上的概率。
的定义域为集合
，集合
．
，并说明理由。
被两平行直线
和
所截得的线段长为9，且直线过点
，求直线
与两坐标轴围成的三角形的面积为3，分别求满足下列条件的直线
.
垂直.相关知识点
推荐套卷
（本小题满分14分）已知圆C的圆心在坐标原点，且与直线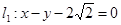相切.
（1）求直线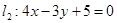被圆C所截得的弦AB的长；
（2）过点G（1,3）作两条与圆C相切的直线，切点分别为M,N，求直线MN的方程；
（3）若与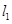直线垂直的直线不过点R（1,-1），且与圆C交于不同的两点P，Q.若∠PRQ为钝角，求直线的纵截距的取值范围．
粤公网安备 44130202000953号