二次函数y=ax2+bx+c(a≠0)的图象如图所示,求:
(1)对称轴是____________;
(2)函数解析式____________;
(3)当x______时,y随x增大而减小;
(4)由图象回答:
当y>0时,x的取值范围_____ _;
当y=0时,x=______ ;
当y<0时,x的取值范围_____ .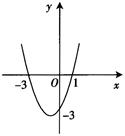
相关知识点
推荐套卷
二次函数y=ax2+bx+c(a≠0)的图象如图所示,求:
(1)对称轴是____________;
(2)函数解析式____________;
(3)当x______时,y随x增大而减小;
(4)由图象回答:
当y>0时,x的取值范围_____ _;
当y=0时,x=______ ;
当y<0时,x的取值范围_____ .