(本题10分)已知:抛物线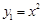 以点C为顶点且过点B,抛物线
以点C为顶点且过点B,抛物线 以点B为顶点且过点C,分别过点B、C作
以点B为顶点且过点C,分别过点B、C作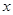 轴的平行线,交抛物线
轴的平行线,交抛物线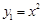 、
、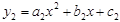 于点A、D,E、F分别为AB、CD中点,连结EC、BF,且AE=BF.
于点A、D,E、F分别为AB、CD中点,连结EC、BF,且AE=BF.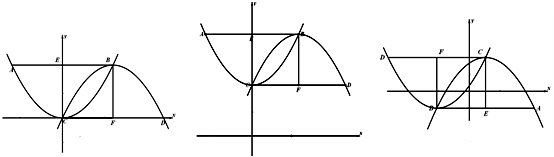
(1)如图1,①求证四边形ECFB为正方形;②求点A的坐标;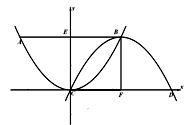
(2)①如图2,若将抛物线“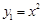 ”改为“
”改为“ ”,其他条件不变,求CD的长;
”,其他条件不变,求CD的长;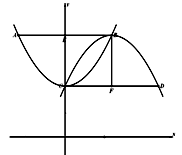
②如图3,若将抛物线“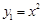 ”改为“
”改为“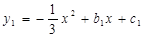 ”,其他条件不变,求
”,其他条件不变,求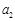 的值;
的值;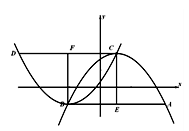
(3)若将抛物线“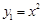 ”改为抛物线“
”改为抛物线“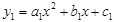 ”,其他条件不变,请用含b2的
”,其他条件不变,请用含b2的
代数式表示b1.
相关知识点
推荐套卷

 ≈1.73
≈1.73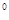 ,∠B=45
,∠B=45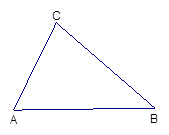

 粤公网安备 44130202000953号
粤公网安备 44130202000953号