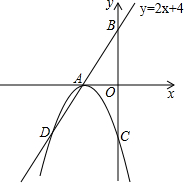如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,﹣4).
(1)求抛物线的解析式;
(2)将抛物线顶点沿着直线AB平移,此时顶点记为E,与y轴的交点记为F,
①求当△BEF与△BAO相似时,E点坐标;
②记平移后抛物线与AB另一个交点为G,则S△EFG与S△ACD是否存在8倍的关系?若有请直接写出F点的坐标.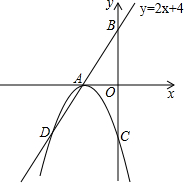
相关知识点
推荐套卷
如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,﹣4).
(1)求抛物线的解析式;
(2)将抛物线顶点沿着直线AB平移,此时顶点记为E,与y轴的交点记为F,
①求当△BEF与△BAO相似时,E点坐标;
②记平移后抛物线与AB另一个交点为G,则S△EFG与S△ACD是否存在8倍的关系?若有请直接写出F点的坐标.