函数y=2cos(ωx+θ)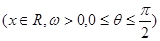
的图象与y轴交于点(0,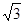 ),且该函数的最小正周期为π.
),且该函数的最小正周期为π.
(1)求θ和ω的值;
(2)已知点A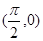 ,点P是该函数图象上一点,点Q(x0,y0)是PA的中点,当y0=
,点P是该函数图象上一点,点Q(x0,y0)是PA的中点,当y0=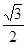 ,x0∈
,x0∈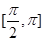 时,求x0的值.
时,求x0的值.
相关知识点
推荐套卷
函数y=2cos(ωx+θ)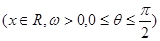
的图象与y轴交于点(0,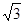 ),且该函数的最小正周期为π.
),且该函数的最小正周期为π.
(1)求θ和ω的值;
(2)已知点A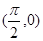 ,点P是该函数图象上一点,点Q(x0,y0)是PA的中点,当y0=
,点P是该函数图象上一点,点Q(x0,y0)是PA的中点,当y0=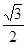 ,x0∈
,x0∈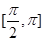 时,求x0的值.
时,求x0的值.