如图，在四棱锥P-ABCD中，PA⊥底面ABCD，PC⊥AD，底面ABCD为梯形，AB∥DC，AB⊥BC，PA＝AB＝BC，点E在棱PB上，且PE＝2EB.
（1）求证：平面PAB⊥平面PCB；
（2）求证：PD∥平面EAC.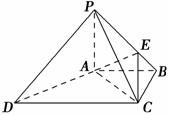
相关试题
(
,
为自然对数的底数).
的单调性;
,函数
在区间
上为增函数,求整数
的最大值.
的最小正周期和单调减区间；
，且
，求
值.
（
）．
时，求函数
在
上的最大值和最小值；
的取值范围.
（
）在区间
上有最大值
和最小值
．设
．
、
的值；
在
上有解，求实数
的取值范围.
的图象与
轴相交于点
，且该函数相邻两零点距离为
．
和
的值；
，
，求
值.
推荐套卷
如图，在四棱锥P-ABCD中，PA⊥底面ABCD，PC⊥AD，底面ABCD为梯形，AB∥DC，AB⊥BC，PA＝AB＝BC，点E在棱PB上，且PE＝2EB.
（1）求证：平面PAB⊥平面PCB；
（2）求证：PD∥平面EAC.
粤公网安备 44130202000953号