已知函数f（x）=f′（1）ex﹣1﹣f（0）x+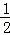
x2，其中e是自然对数的底数，f′（x）为f（x）的导函数．
（1）求函数f（x）的解析式；
（2）若函数g（x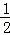）=x2+a与函数f（x）的图象在区间[﹣1，2]上恰有两个不同的交点，求实数a的取值范围．
中，
是
的中点，求证：
平面
中，点
分别是棱
的中点。求证：
平面
；
的单调递减区间为
,求函数
,
恒成立,求实数
的取值范围．
，
的单调区间；
时，
．
，当
时，函数
有极值－
．求函数推荐套卷
已知函数f（x）=f′（1）ex﹣1﹣f（0）x+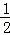x2，其中e是自然对数的底数，f′（x）为f（x）的导函数．
（1）求函数f（x）的解析式；
（2）若函数g（x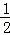）=x2+a与函数f（x）的图象在区间[﹣1，2]上恰有两个不同的交点，求实数a的取值范围．
粤公网安备 44130202000953号