已知双曲线y=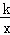
（k＞0），过点M（m，m）（m＞
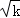）作MA⊥x轴，MB⊥y轴，垂足分别是A和B，MA、MB分别交双曲线y=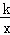（k＞0）于点E、F。
（1）若k=2，m=3，求直线EF的解析式；
（2）O为坐标原点，连接OF，若∠BOF=22.5°，多边形BOAEF的面积是2，求k值。
相关试题
，请写出所有符合条件的两位数．
是方程组
的解，求
的值．
克，每只黑球和白球的质量各是多少克？
的解
与
相等，求
的值．
，“
”和“△”表示被污染的内容，他着急，翻开书后面的答案，这道题的解是
你能帮助他补上“相关知识点
推荐套卷
已知双曲线y=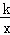（k＞0），过点M（m，m）（m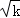＞）作MA⊥x轴，MB⊥y轴，垂足分别是A和B，MA、MB分别交双曲线y=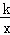（k＞0）于点E、F。
（1）若k=2，m=3，求直线EF的解析式；
（2）O为坐标原点，连接OF，若∠BOF=22.5°，多边形BOAEF的面积是2，求k值。
粤公网安备 44130202000953号