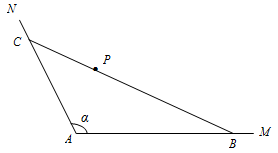
如图（示意），公路AM、AN围成的是一块顶角为α的角形耕地，其中tanα＝－2．在该块土地中P处有一小型建筑，经测量，它到公路AM，AN的距离分别为3km，km．现要过点P修建一条直线公路BC，将三条公路围成的区域ABC建成一个工业园．为尽量减少耕地占用，问如何确定B点的位置，使得该工业园区的面积最小？并求最小面积．
，
，
，
．求证
．
中，直线
经过点P（0，1），曲线
的方程为
，若直线
，
两点，求
的值．
把直线
变换为另一条直线
，试求实数
值．
的两弦
和
交于点
，
，
交
的延长线于点
．求证：△
∽△
．
，
，且
，
．
，证明数列{bn}是等比数列；
，求集合
．推荐套卷
如图（示意），公路AM、AN围成的是一块顶角为α的角形耕地，其中tanα＝－2．在该块土地中P处有一小型建筑，经测量，它到公路AM，AN的距离分别为3km，km．现要过点P修建一条直线公路BC，将三条公路围成的区域ABC建成一个工业园．为尽量减少耕地占用，问如何确定B点的位置，使得该工业园区的面积最小？并求最小面积．
粤公网安备 44130202000953号