已知曲线C的参数方程是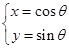
( θ为参数 )，以直角坐标系xoy的原点为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为ρ(cosθ+ sinθ) = 4
（Ⅰ）试求曲线C上任意点M到直线l的距离的最大值；
（Ⅱ）设P是l上的一点，射线OP交曲线C于R点，又点Q在射线OP上，且满足|OP|·|OQ|=|OR|2，当点P在直线l上移动时，试求动点Q的轨迹.
相关试题
÷5=
÷4=
÷2=
÷3=
÷
=
÷
=
÷
÷
=
= 15÷
=
÷
=
÷
=
×
×
=
+
= 1﹣
=
=
=
=
=
=
=
= 1.05×4= 268÷14×0=
= 306﹣16= 5.1+0.09=
﹣
=
÷
= 9
÷3=
×3=
÷5=
×1.6= 15×60%= 25×40%=
=
=
=
=
=
=
=
=
=相关知识点
推荐套卷
已知曲线C的参数方程是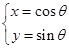 ( θ为参数 )，以直角坐标系xoy的原点为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为ρ(cosθ+ sinθ) = 4
（Ⅰ）试求曲线C上任意点M到直线l的距离的最大值；
（Ⅱ）设P是l上的一点，射线OP交曲线C于R点，又点Q在射线OP上，且满足|OP|·|OQ|=|OR|2，当点P在直线l上移动时，试求动点Q的轨迹.
粤公网安备 44130202000953号