如图（1），E是正方形ABCD的边BC上的一个点（E与B、C两点不重合），过点E作射线EP⊥AE，在射线EP上截取线段EF，使得EF=AE；过点F作FG⊥BC交BC的延长线于点G．
（1）求证：FG=BE；
（2）连接CF，如图（2），求证：CF平分∠DCG；
（3）当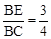
时，求sin∠CFE的值．
相关试题
推荐套卷
如图（1），E是正方形ABCD的边BC上的一个点（E与B、C两点不重合），过点E作射线EP⊥AE，在射线EP上截取线段EF，使得EF=AE；过点F作FG⊥BC交BC的延长线于点G．
（1）求证：FG=BE；
（2）连接CF，如图（2），求证：CF平分∠DCG；
（3）当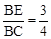时，求sin∠CFE的值．
粤公网安备 44130202000953号