已知二次函数:(1)y=x2+x-2 (2)y=x2-6x+9 (3)y=x2-x+1的图象如图所示,观察图象解决下列问题:
(1)以上二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?
(2)当x取公共点的横坐标时,二次函数的值是多少?由此,你能直接写出相应的一元二次方程的根吗?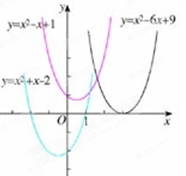
相关知识点
推荐套卷
已知二次函数:(1)y=x2+x-2 (2)y=x2-6x+9 (3)y=x2-x+1的图象如图所示,观察图象解决下列问题:
(1)以上二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?
(2)当x取公共点的横坐标时,二次函数的值是多少?由此,你能直接写出相应的一元二次方程的根吗?