中国“蛟龙”号深潜器目前最大深潜极限为7062.68米。某天该深潜器在海面下1800米处作业（如图），测得正前方海底沉船C的俯角为45°，该深潜器在同一深度向正前方直线航行2000米到B点，此时测得海底沉船C的俯角为60°.
（1）沉船C是否在“蛟龙”号深潜极限范围内？并说明理由;
（2）由于海流原因，“蛟龙”号需在B点处马上上浮，若平均垂直上浮速度为2000米/时，求“蛟龙”号上浮回到海面的时间.（参考数据：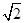
≈1.414，
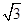≈1.732）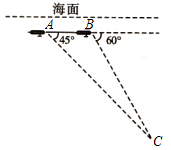
相关试题
如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A (3，2)、B(1，3)。△AOB绕点O 逆时针旋转90°后得到△A1OB1.
（1）画出旋转后的图形；
（2）求线段OB在旋转过程中所扫过的图形面积（写过程）。
随着市民环保意识的增强，节庆期间烟花爆竹销售量逐年下降．某市2012年销售烟花爆竹20万箱，到2014年烟花爆竹销售量为9.8万箱．求该市2012年到2014年烟花爆竹年销售量的平均下降率．
相关知识点
推荐套卷
粤公网安备 44130202000953号