某中学社团部志愿者协会共有6名男同学，4名女同学. 在这10名同学中，3名同学来自动漫社，其余7名同学来自摄影社、话剧社等其他互不相同的七个社团. 现从这10名同学中随机选取3名同学，到社区参加志愿活动（每位同学被选到的可能性相同）.
（Ⅰ）求选出的3名同学是来自互不相同社团的概率；
（Ⅱ）设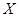
为选出的3名同学中女同学的人数，求随机变量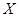的分布列和数学期望.
相关试题
中，
分别是上、下底面的中心．已知
，
．
[（x1－
）2＋（x2－推荐套卷
某中学社团部志愿者协会共有6名男同学，4名女同学. 在这10名同学中，3名同学来自动漫社，其余7名同学来自摄影社、话剧社等其他互不相同的七个社团. 现从这10名同学中随机选取3名同学，到社区参加志愿活动（每位同学被选到的可能性相同）.
（Ⅰ）求选出的3名同学是来自互不相同社团的概率；
（Ⅱ）设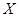为选出的3名同学中女同学的人数，求随机变量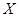的分布列和数学期望.
粤公网安备 44130202000953号