已知抛物线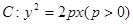 ,
,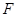 为抛物线
为抛物线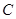 的焦点,
的焦点, 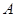 为抛物线
为抛物线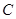 上的动点,过
上的动点,过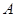 作抛物线准线
作抛物线准线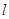 的垂线,垂足为
的垂线,垂足为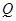 .
.
(1)若点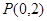 与点
与点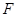 的连线恰好过点
的连线恰好过点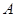 ,且
,且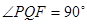 ,求抛物线方程;
,求抛物线方程;
(2)设点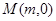 在
在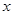 轴上,若要使
轴上,若要使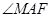 总为锐角,求
总为锐角,求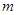 的取值范围.
的取值范围.
相关知识点
推荐套卷
已知抛物线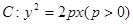 ,
,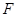 为抛物线
为抛物线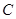 的焦点,
的焦点, 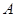 为抛物线
为抛物线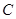 上的动点,过
上的动点,过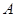 作抛物线准线
作抛物线准线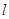 的垂线,垂足为
的垂线,垂足为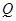 .
.
(1)若点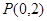 与点
与点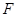 的连线恰好过点
的连线恰好过点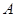 ,且
,且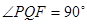 ,求抛物线方程;
,求抛物线方程;
(2)设点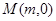 在
在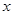 轴上,若要使
轴上,若要使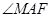 总为锐角,求
总为锐角,求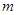 的取值范围.
的取值范围.