某教室有4扇编号为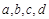
的窗户和2扇编号为
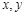的门，窗户
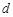敞开，其余门和窗户均被关闭．为保持教室空气流通，班长在这些关闭的门和窗户中随机地敞开2扇．
（Ⅰ）记“班长在这些关闭的门和窗户中随机地敞开2扇”为事件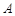
，请列出事件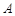包含的基本事件；
（Ⅱ）求至少有1扇门被班长敞开的概率．
相关试题
的极小值为-8，其导函数的图象过点
，如图所示
的解析式
都有
恒成立，求实数的m取值范围。
，其中a为正实数．
时，求f（x）的极值点；
在
处有极小值-1，求
的单调区间.
，y＝2－x，y＝－
x围成图形的面积．
对一切
，都有
，且
时，
，
。
上的最大值和最小值。推荐套卷
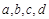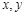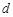某教室有4扇编号为的窗户和2扇编号为的门，窗户敞开，其余门和窗户均被关闭．为保持教室空气流通，班长在这些关闭的门和窗户中随机地敞开2扇．
（Ⅰ）记“班长在这些关闭的门和窗户中随机地敞开2扇”为事件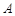，请列出事件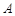包含的基本事件；
（Ⅱ）求至少有1扇门被班长敞开的概率．
粤公网安备 44130202000953号